Stampa 3D per metamateriali meccanici: progettazione pseudo-meccanismo e unità multistabili
Nitin Singh e Martin van Hecke, entrambi ricercatori nei Paesi Bassi, esplorano gli pseudo-meccanismi e la stampa 3D dei relativi elementi costitutivi. I loro risultati sono stati pubblicati nel recente progetto ” Progettazione di pseudo-meccanismi e unità multistabili per metamateriali meccanici “.
Essendo elementi rigidi e flessibili collegati tra loro ma che mostrano un movimento a “energia zero”, i meccanismi sono fondamentali per aspetti come i supporti inceppati e le reti a molla, svolgendo un ruolo importante nell’ingegneria meccanica. I meccanismi sono fondamentali nella progettazione di strumenti robotici di base come le pinze, mentre i metamateriali basati su meccanismi derivano da tali progetti ma sono composti da componenti più flessibili che collegano parti rigide.
“Eccitato” da forze esterne, può emergere una varietà di proprietà uniche:
Parametri di risposta negativa
Shape-morphing
Polarizzazione topologica
programmabilità
multistability
Self-pieghevole
Negli pseudomeccanismi troviamo elementi accoppiati flessibili che mostrano movimento a basso costo energetico. I ricercatori osservano che possono diffondersi attraverso l’ottimizzazione dello sciame di particelle.
“La nostra scoperta principale è che la maggior parte dei PM sono geometricamente molto distinti dai meccanismi reali; la maggior parte dei PM non sono semplicemente meccanismi perturbati, ma i PM permeano lo spazio di progettazione molto lontano dal sottospazio dei meccanismi reali “, spiegano i ricercatori. “Estendiamo le nostre tecniche di ricerca per ottenere unità multistabili e realizzarle con la stampa 3D”.
In termini di sistemi, il team di ricerca ha considerato gruppi di quadrilateri collegati da cerniere. Quadrati di dimensioni uguali consistevano in sistemi a modalità zero sottostanti numeri di metamateriali meccanici.
“Le generalizzazioni, compresi i regolari tetti di quadrati, rettangoli o 3D di dimensioni alternate, sono ben note”, hanno affermato i ricercatori. “Le condizioni per tali raccolte di quadrilateri per formare un meccanismo sono semplici”.
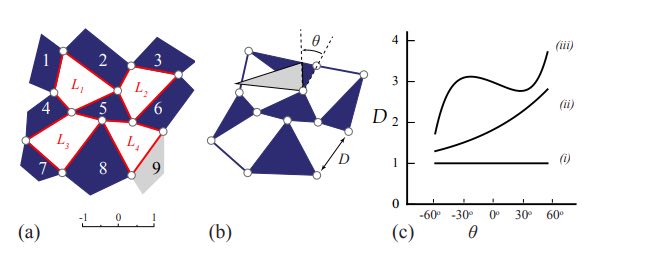
a) Unità completa costituita da nove quadrilateri rigidi (1-9), collegati da dodici cerniere flessibili {x12, x23,. . . } (cerchie). Questa unità può anche essere vista come quattro collegamenti collegati a quattro barre Li. (b) Unità diluita. (c) A seconda del disegno dei quadrilateri (1-8), il movimento caratteristico dell’unità diluita, D (θ), può essere (quasi) costante (i), una funzione monotonica (ii) o una funzione non monotonica (iii).
Il progetto per ottimizzazione dello sciame di particelle includeva un algoritmo inteso a ridurre la funzione di costo, identificando i “minimi profondi” in un paesaggio accidentato, usando uno “sciame” di particelle destinato a rappresentare numerosi progetti.
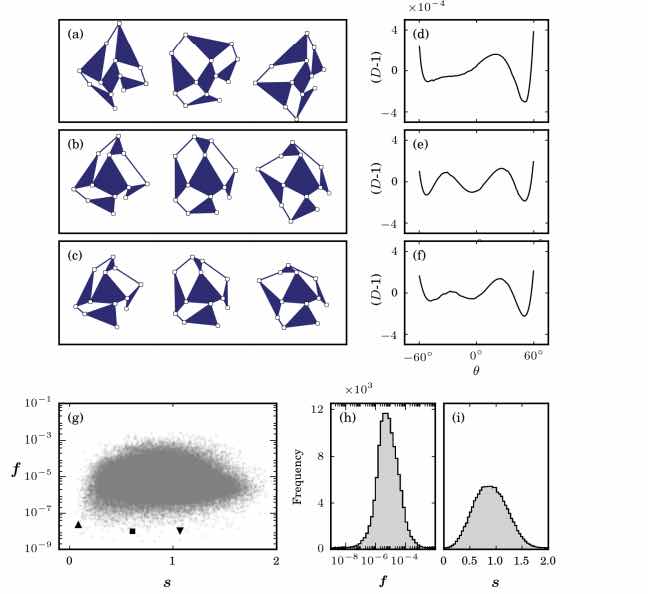
(ac) Tre esempi di unità diluite per le quali D (θ) è quasi costante e uguale a 1, per θ ∈ [−60◦, 60◦], per [f, s] = 2,26 × 10−8, 0,084 (a ); 9,88 × 10−9, 0,611 (b); e 1,04 × 10−8, 1,06 (c). Le tre istantanee in ciascun pannello corrispondono a θ = −60◦, 0◦ e 60◦. (df) grafici corrispondenti di D – 1 vs θ; notare la scala. (g) Scatter-plot di f vs s, dove i simboli uptriangle, square e downtriangle indicano rispettivamente i valori dei parametri mostrati nei pannelli (ac). (f, g) Distribuzioni di f e s.
Le celle di unità flessibili generiche offrono unità diluite con una curva target di Dt1 (θ) = 1 e PSO distribuito per i progetti con valori bassi di f .
“I nostri risultati suggeriscono un’organizzazione complessa dello spazio di progettazione. Per ottenere informazioni su questa struttura, abbiamo esplorato se il valore di f aumenta se una determinata soluzione x0 viene perturbata in modo casuale “, hanno affermato i ricercatori. “In particolare, generiamo 1000 vettori casuali a 24 dimensioni dx con ciascuna voce uniformemente distribuita tra -1 e 1, e quindi calcoliamo f (x0 + εdx) per un intervallo di ε.”
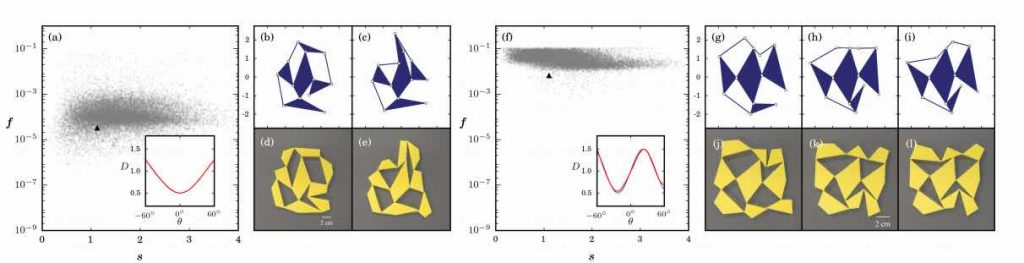
(a) Grafico a dispersione [18000 punti] di fa per la funzione bersaglio Dt (θ) = 1 + 0,5 sin (2θ + π / 2). Inserto: l’obiettivo e D (θ) realizzati per f = 3.2 × 10−5, s = 1.12 (triangolo nel riquadro (a)) sono praticamente indistinguibili. (b, c) Unità potata corrispondente per θ = ± 60◦, dove D ≈ 1 (d, e) Unità bistabile flessibile stampata in 3D corrispondente in entrambi i suoi stati stabili. (f) Grafico a dispersione [18000 punti] di f per una funzione bersaglio Dt (θ) = 1 + 0,5 sin (4θ). Inserto: l’obiettivo e D (θ) realizzati per f = 6,7 × 10−3, s = 1,10 (triangolo nel pannello (g)) sono praticamente indistinguibili. (gi) Unità di potatura corrispondente per θ = −45◦, 0◦, 45◦, dove D ≈ 1. (jl) unità tristable stampata in 3D in tutti e tre gli stati stabili.
I ricercatori hanno anche notato che tutti i quad di esempio erano bistabili e trattabili, offrendo configurazioni come quella inizialmente proiettata. Un nono quad di lunghezza adeguata è stato aggiunto con unità complete stampate in 3D usando Filaflex.
“Concettualmente, il passaggio da un meccanismo 2 × 3 a uno pseudo meccanismo 3 × 3 potrebbe essere simile a quello da uno pseudo meccanismo 3 × 3 a uno 3 × 4, ma è una domanda aperta su come lo spazio di progettazione si evolva per dimensioni sempre maggiori sistemi “, hanno concluso i ricercatori.
“Un’ulteriore possibilità intrigante sorge, ad esempio, per il soffietto: mentre il volume di un poliedro non può cambiare mentre si flette, in pratica gli pseudo-meccanismi possono funzionare ugualmente bene. Inoltre, ci chiediamo se gli pseudomeccanismi possano imitare un equivalente della polarizzazione topologica, delle modalità dei bordi e dei cornermode osservati nei metamateriali meccanici topologicamente non banali che si basano su meccanismi reali. Infine, il nostro spazio di progettazione ha solo dimensioni moderate e ottenere progetti non banali è relativamente economico dal punto di vista computazionale. Ciò rende i nostri progetti particolarmente adatti per testare se le tecniche di apprendimento automatico sarebbero adatte, in primo luogo, ad essere addestrate per distinguere i meccanismi pseudo “buoni” da “cattivi”, in secondo luogo, per rilevare e classificare progetti multistabili e, in terzo luogo, possono essere utilizzati per accelerare la progettazione di tali strutture. “
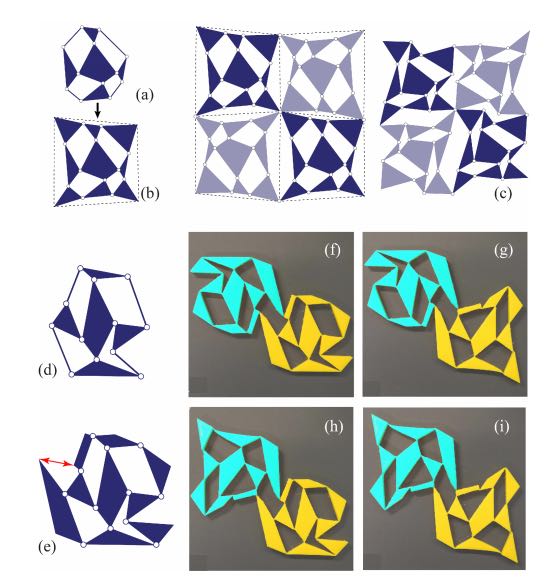
(ab) Progettazione di un PM potenziato sostituendo le barre esterne con triangoli. (c) Una piastrellatura sfalsata di tali PM ha una modalità di incernieramento morbido. (d) Design bistabile. (e) Progettazione aumentata in cui la distanza della distanza (freccia rossa) ha la stessa lunghezza in entrambi gli stati stabili. (fi) Due celle di unità 3D stampabili bistabili collegate (verde, giallo) possono essere scattate tra quattro diversi stati stabili (aggiunto colore verde falso per visibilità).
